Soit un triangle équilatéral de coté de longueur c.
Exprime son aire en fonction de c.
Engage les mathématiques
Quelle(s) mathématique (s) aurais-tu envie de mobiliser ?
Utilise des mathématiques
Lemme 1 (à admettre ou démontrer lorsque tu seras en études supérieures de mathématiques)
Soit un polygone simple et une droite coupant le polygone en deux parties.
Alors, l'aire du polygone est la somme des aires des parties.
Lemme 2 (théorème de Pythagore) (à admettre ou à démontrer) [1]
Soit un triangle ABC rectangle en A. Alors BC² = AB² + AC²
Lemme 3 ( à démontrer)
Soit un triangle. Soit A un des sommets et BC le coté opposé. Soit H l'intersection de la hauteur tirée de A. Alors, l'aire d'un triangle ABC est égal au demi produit AH x BC.
Lemme 4 (à démontrer)
Soit un triangle ABC isocèle en A. Alors, la hauteur issue de A est un axe de symétrie du triangle ABC.
[1]Théorème de Pythagore - démonstration d'Euclide et démonstration "indienne", Le point , la règle et la droite
Implémente les mathématiques
Voici une animation réalisée avec le logiciel Scratch. Tu pourras jouer avec le code sur le site Scratch [1].
[1] https://scratch.mit.edu/projects/740274160
Explore d'autres mathématiques
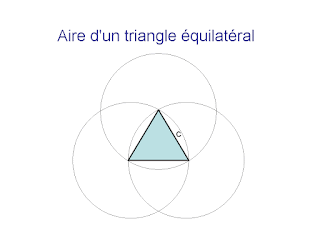
Pour exprimer l'aire d'un triangle équilatéral, tu as mobilisé plusieurs lemmes que tu as orchestrés. Voici deux autres exercices : l'aire d'un hexagone [1] et l'aire d'un pentagone [2]
[1] Aire d'un hexagone régulier , Le point, la règle et la droite
[2] Aire d'un pentagone régulier, Le point, la règle et la droite
Réponse :
L'aire d'un triangle équilatéral de coté c est c² √3/4